mathadomicile.fr
Tans Generator & Solver
1. The default mode of the program is mode 'Research shapes' which is
the place to create shapes to be matched with the tanset in the 'Play'
mode. You may select here the number of triangles in your shapes (this
number should be equal to the tanset number of triangles for its
ability to match the shapes) and also the shape type : convex or not,
with a center of symmetry or an axis... When you validate your choice
the program starts the research wich could take some time if you are
working with a great number of triangles or sides. When the research
ends, it displays the result by pages of 8 shapes. These shapes are
those you may try to match with your tanset if you press the 'Record
shapes' button.
2. In the 'Choose a tanset' mode, you may select the tans of your
game (tanset) to play with in the 'Play' mode. The total area of the
tans should fit the number of triangles of your recorded shapes. You
may change the color of each tan, erase a tan from the tanset or
select a well-known tanset (Tangram, Chie-no-ita, etc.). At this
stage, you may also change the way of computing the Z score. When your
choice is done, you press the 'Choose' button and then enter the
'Play' mode.
3. After shapes have been recorded and a tanset is selected, you may try to play with the tans, in order to match the recorded shapes in the 'Play' mode. The button 'Next recorded shape' give you the shapes one by one. It is also possible to create here free shapes to be matched (it is colored in yellow when area become equal to the tanset area and when the constitution of the shape obeys to the tans rules, in red if the area is ok but not the rules). The button 'Progressive Solution' starts the solving program and dispays the research of the solution step by step. You may try that way to match all the recorded shapes and all the free shapes you create (see above how to create a shape with a hole that is matched by the 'Chie-no-ita tanset'). If you want to see how many recorded shapes are matched with the tanset, press the 'Bilan tanset' button, you then reach the last mode. You may also play in a simple way, trying by yourself to match the shapes using all the different tans : each tan could be moved when you hold the zero point (coloring in a cyan cross when you come close to it) ; a right clic make it turn clokwise, middle clic turn counterclockwise, double clic make a flip.
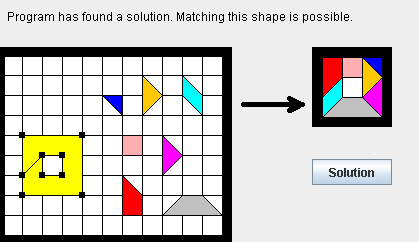
4. The 'Find a better tanset' mode is the place to see the recorded
shapes that could be matched by the tanset (a solution is given if
any). This mode also computs the Z score of the tanset wich is suppose
to measure the ability of the tanset to match the shapes in an
aesthetic and ludic fashion (maximum differences between tans, minimum
number of tans). You may read more about this Z score in our
old page about Tangram family or, if you read french, in the
recent one. If you press here the ![]() button you starts the research of a
better tanset amongst the tansets of analogous structure. You may look
for a better tanset (better Z score) or even look for the best one. In
the java console window, you may follow the research according the Z
parameter you have settled. If you write Z=-1you will have a faster
research and also better for your computer (a delay of 10 s is added
every 1000 tansets). You may choose to use only convex tans (this has
an effect on the treatment time...), you may also change the
structure: all the various structures of the same number of tans as
your structure are dispayed on a list. You just have to select one of
these structures -the tanset count is thus displayed- and validate
this choice. Here again you could choose to research a tanset that has
a better Z score, or use all the possible tansets (beware of their
number that could be great!)
button you starts the research of a
better tanset amongst the tansets of analogous structure. You may look
for a better tanset (better Z score) or even look for the best one. In
the java console window, you may follow the research according the Z
parameter you have settled. If you write Z=-1you will have a faster
research and also better for your computer (a delay of 10 s is added
every 1000 tansets). You may choose to use only convex tans (this has
an effect on the treatment time...), you may also change the
structure: all the various structures of the same number of tans as
your structure are dispayed on a list. You just have to select one of
these structures -the tanset count is thus displayed- and validate
this choice. Here again you could choose to research a tanset that has
a better Z score, or use all the possible tansets (beware of their
number that could be great!)
Using all these possibilities given by the program, we have founded
this square dissection in 9 tans counting 32 triangles which is able
to match 33 convex shapes and have this Z score = 35. Compare with the
Z = 12 of the Tangram wich is only able to match 13convex shapes... Here are two
square dissections in 9 tans counting 50 triangles : the first
contains only convex tans, is able to match 45 convex shapes and is
granted with this Z score = 46!
Here are two
square dissections in 9 tans counting 50 triangles : the first
contains only convex tans, is able to match 45 convex shapes and is
granted with this Z score = 46! , the second contains a not convex
tan, is able to match 48 convex shapes and is granted with this Z
score = 49!
, the second contains a not convex
tan, is able to match 48 convex shapes and is granted with this Z
score = 49! This last square dissection in 10 tans counting 64 triangles is able
to match 60 convex shapes and is granted with this Z score = 60!!
This last square dissection in 10 tans counting 64 triangles is able
to match 60 convex shapes and is granted with this Z score = 60!!
This program has been created for mathadomicile.fr with the help and
ideas and procedures of Eric Warsop and his excellent program Wintanxx
describe in this guide. Regards to your
work Eric!
Regards to your
work Eric!
A lot of good things also came from the reading, the use and
contribution to this wonderfull applet
of Sergio Antoy. Thanks a lot for your encouragements!
Thanks a lot for your encouragements!
This version (S6.0) is in validation mode, far from the perfection.
Thanks to your suggestions or remarks
for a future better version... You may look at the
code or run it directly (better display) or change it as you
want.
For those who are interested in the coding, the different ways of
digitization of the tans, or how the program works, we wrote here some explanations. Sorry for my bad
english..
New feature for last versions : Different threads are used to comput
the shapes or solutions and for the dispay. So, a progress bar could
be dispayed and new shapes or new solutions may be viewed during the
comput process. Minor changes are also added : possible change of the
Z codification.
PM

