mathadomicile.fr
Puzzles de la famille du Tangram
|
L'applet de Sergio Antoy permet de jouer en ligne avec plusieurs puzzles de la famille du Tangram : Tangram, Chie-no-Ita, Pythagoras, Revathi, Heptex et bien d'autres.  |
Wintanxx, Le programme d'Eric Wharshop n'est pas une applet mais un programme executable (.exe) dont on décompresse cette archive. Ce programme dispose d'une notice online en anglais.  |
L'applet de Mathadomicile permet de créer des puzzles, d'y jouer en ligne, d'avoir les solutions et d'effectuer des recherches pour trouver de 'meilleurs' puzzles.  |
Publié en 2014 sous licence libre*, le livre  de 340 pages "Tangram Evolutif" contient toutes mes connaissances sur
le Tangram, ce jeu des sept plaquettes ingénieuses. Pour la
plupart, elles sont le résultat d'un travail de recherche qui s'est
étendu sur plusieurs années, en partie par une collaboration avec
Ronald Read, ce grand pionnier du Tangram. Suite à mes premiers
travaux, encouragé par J.-P. Delahaye à écrire un livre sur le sujet,
j'ai rédigé "L'Univers du Tangram". Ce livre qui devait paraître en
2013 a fait l'objet de relectures, corrections et mises en page de
l'éditeur, mais il est resté bloqué à ce stade final chez celui-ci,
pour une raison inconnue et indépendante de ma volonté. Ma recherche
ayant produit entretemps de nouveaux résultats, j'avais commencé un
second livre sur le sujet, et comme la publication du premier
n'avançait plus, j'en ai repris les principaux éléments, afin que ce
second livre soit à peu prés complet sur le sujet, du moins pour ce
que je pouvais en dire. Pour ne pas recommencer l'expérience
frustrante d'une nouvelle aventure éditoriale, j'ai choisi cette forme
de publication. N'étant pas éditeur, ce livre n'a sans doute pas la
mise en page idéale et son texte, n'ayant pas été relu suffisamment,
contient sans doute encore quelques erreurs (malgré l'expertise
orthographique de mon père). N'étant pas non plus informaticien ou
mathématicien, certains défauts plus profonds se sont peut-être aussi
glissés à mon insu dans ces lignes. Pour toutes ces raisons, je
requière l'indulgence de mes lecteurs et accepte toute
forme de critique ou suggestion dans ma boîte mail. La suite de cette
page web conserve une des formes initiales du texte qui a été mise en
ligne en novembre 2010. Bonne lecture et bon voyage dans l'univers du
Tangram!
de 340 pages "Tangram Evolutif" contient toutes mes connaissances sur
le Tangram, ce jeu des sept plaquettes ingénieuses. Pour la
plupart, elles sont le résultat d'un travail de recherche qui s'est
étendu sur plusieurs années, en partie par une collaboration avec
Ronald Read, ce grand pionnier du Tangram. Suite à mes premiers
travaux, encouragé par J.-P. Delahaye à écrire un livre sur le sujet,
j'ai rédigé "L'Univers du Tangram". Ce livre qui devait paraître en
2013 a fait l'objet de relectures, corrections et mises en page de
l'éditeur, mais il est resté bloqué à ce stade final chez celui-ci,
pour une raison inconnue et indépendante de ma volonté. Ma recherche
ayant produit entretemps de nouveaux résultats, j'avais commencé un
second livre sur le sujet, et comme la publication du premier
n'avançait plus, j'en ai repris les principaux éléments, afin que ce
second livre soit à peu prés complet sur le sujet, du moins pour ce
que je pouvais en dire. Pour ne pas recommencer l'expérience
frustrante d'une nouvelle aventure éditoriale, j'ai choisi cette forme
de publication. N'étant pas éditeur, ce livre n'a sans doute pas la
mise en page idéale et son texte, n'ayant pas été relu suffisamment,
contient sans doute encore quelques erreurs (malgré l'expertise
orthographique de mon père). N'étant pas non plus informaticien ou
mathématicien, certains défauts plus profonds se sont peut-être aussi
glissés à mon insu dans ces lignes. Pour toutes ces raisons, je
requière l'indulgence de mes lecteurs et accepte toute
forme de critique ou suggestion dans ma boîte mail. La suite de cette
page web conserve une des formes initiales du texte qui a été mise en
ligne en novembre 2010. Bonne lecture et bon voyage dans l'univers du
Tangram!
La version papier de ce livre est disponible (demander à l'auteur).
PM, mai 2014
*Tangram Evolutif est
mis à disposition selon les termes de la licence Creative Commons Attribution 4.0 International.
Une extension du sujet a vu le jour en 2022 avec les formes en duos
et celles qui font leur solo. Lisez cet article qui ne traite pas que
du Tangram (le puzzle Chie-no-ita, version japonaise du jeu chinois
est le point de départ de cette découverte). Télecharger cet
article (21 pages).
avec les formes en duos
et celles qui font leur solo. Lisez cet article qui ne traite pas que
du Tangram (le puzzle Chie-no-ita, version japonaise du jeu chinois
est le point de départ de cette découverte). Télecharger cet
article (21 pages).
Le Tangram est un très ancien et très connu puzzle géométrique, classé souvent parmi les "casse-têtes" car les figures
proposées ne sont pas faciles à reconstituer. Il est composé de sept
pièces aux formes dérivées du demi-carré (carré coupé selon une de ses
diagonales ou triangle rectangle-isocèle). Nous nous intéressons dans
cette page aux puzzles de la famille du Tangram, c'est-à-dire
constitués avec des pièces du même genre que celles du Tangram.
géométrique, classé souvent parmi les "casse-têtes" car les figures
proposées ne sont pas faciles à reconstituer. Il est composé de sept
pièces aux formes dérivées du demi-carré (carré coupé selon une de ses
diagonales ou triangle rectangle-isocèle). Nous nous intéressons dans
cette page aux puzzles de la famille du Tangram, c'est-à-dire
constitués avec des pièces du même genre que celles du Tangram.
Ces pièces sont des polygones composés de demi-carrés aux bords confondus qui ont été appelés polyabolos. Les polyabolos contiennent toutes les formes différentes obéissant à ces règles. En cherchant toutes les combinaisons possibles de n demi-carrés on trouve l'ensemble des n-abolos. Ainsi il y a 1 monoabolo (le demi-carré), 3 diabolos (2 demi-carrés assemblés), 4 triabolos (3 demi-carrés), 14 tetrabolos, 30 pentabolos, 107 hexabolos, etc. Ces nombres augmentent très vite avec le nombre n de demi-carrés qui les composent.
En prenant 7 polyabolos totalisant une aire de 16 demi-carrés, on se
retrouve avec un puzzle très comparable au Tangram. Mais d'autres
puzzles assez proches nous intéressent aussi : les puzzles à 5, 6 ou 8
pièces sont des proches cousins. Nous avons choisi de nous limiter
dans cette étude aux puzzles ayant moins de 12 pièces. Le nombre de
demi-triangles totalisé par les pièces du puzzle n'est pas un
caractère limitatif non plus, nous avons choisi d'étudier tous les
puzzles possibles jusqu'à 100 demi-carrés. Ces contraintes nous ont
davantage été dictées par des raisons techniques (taille des tableaux
utilisés par le programme, temps de calcul des recherches) que par des
considérations dogmatiques.
 Les 7 pièces du Tangram réussissent à reconstituer un grand carré
tandis que d'autres puzzles de 7 pièces totalisant 16 demi-carrés n'y
parviennent pas comme celui que nous avons baptisé TTPr (voir un peu
plus bas). Nous nous intéressons spécialement aux puzzles qui peuvent
reconstituer un carré car déjà, le carré est la forme la plus pratique
pour le rangement. Très symétrique et compacte, cette forme est aussi
la plus naturelle et fréquente dans notre vie courante. Notre
recherche pourrait presque s'intituler "recherche des dissections du
carré en morceaux polyaboliques" mais ce serait discriminatoire
vis-à-vis des autres formes. Nous verrons dans la suite que nous avons
favorisé dans notre recherche les puzzles qui arrivent à reconstituer
le carré sans exclure les autres.
Les 7 pièces du Tangram réussissent à reconstituer un grand carré
tandis que d'autres puzzles de 7 pièces totalisant 16 demi-carrés n'y
parviennent pas comme celui que nous avons baptisé TTPr (voir un peu
plus bas). Nous nous intéressons spécialement aux puzzles qui peuvent
reconstituer un carré car déjà, le carré est la forme la plus pratique
pour le rangement. Très symétrique et compacte, cette forme est aussi
la plus naturelle et fréquente dans notre vie courante. Notre
recherche pourrait presque s'intituler "recherche des dissections du
carré en morceaux polyaboliques" mais ce serait discriminatoire
vis-à-vis des autres formes. Nous verrons dans la suite que nous avons
favorisé dans notre recherche les puzzles qui arrivent à reconstituer
le carré sans exclure les autres.
Il est possible de disséquer un carré avec des polyabolos si ceux-ci totalisent un certain nombres n de demi-carrés. En totalisant 2, 4, 8, 16, 18, 32, 36, 50, 64 ou 100 demi-carrés, la reconstitution d'un grand carré est théoriquement possible alors que c'est impossible avec d'autres valeurs de n. Ces nombres sont issus de deux séries de nombres : 2n² et 4n² selon que l'on reconstitue un grand carré ayant le côté (2n²) ou la diagonale (4n²) du petit demi-carré unitaire comme unité. La plupart des puzzles connus de la famille du Tangram sont des dissections du carré d'aire 16 demi-carrés. Nous envisagerons les autres dissections possibles du carré pour plusieurs raisons que nous allons examiner maintenant.
Le carré n'est pas la seule figure convexe réalisable avec les pièces
du Tangram. En 1942, F.T.Wang et C.C.Hsiung montraient que 13 figures
convexes seulement sont réalisables avec les pièces du Tangram sur les
20 différentes formes convexes théoriquement possibles avec une aire
de 16 demi-carrés. Les 20 formes convexes ci-dessus sont les seules
qui ont une aire égale à 16 demi-carrés et qui sont reconstituables
avec 16 demi-triangles. Tout un chacun peut facilement vérifier cela
en crayonnant sur du papier quadrillé par exemple. Notre programme
effectue ce travail en quelques dixièmes de secondes : il essaie
toutes les possibilités pour qu'un polygone aie une aire de 16
demi-carrés et des angles compatibles avec les polyabolos (45°, 90° et
135° pour les convexes).
 Vous pouvez reconstituer 13 figures convexes avec le Tangram (voir
illustration ci-contre), mais d'autres puzzles de 7 pièces totalisant
16 demi-carrés parviennent à en réaliser davantage sur les 20
théoriquement possibles. le
jeu de Revathi*, Chie-no-ita, Cocogram et Heptex en réalisent
respectivement 15, 16, 16 et 19. D'autres puzzles connus en réalisent
moins que 13 : Pythagoras en reconstitue 12 et Regulus en reconstitue
7 seulement. La forme de certaines pièces empêche, par leur seule
présence, la réalisation de certaines formes convexes. Ainsi, pour le
Tangram, c'est la présence des grands demi-triangles qui empêche la
reconstitution de 4 formes (les formes 2, 5, 8 et 13 selon leur ordre
d'apparition dans le programme). Pythagoras, Regulus et Cocogram sont
eux aussi empéchés de reconstituer ces mêmes formes (2, 5, 8 et 13)
par leur plus encombrante pièce mais restent très différents dans leur
capacité à reconstituer des formes convexes. Ce n'est donc pas la
présence d'une grosse pièce qui révèle cette capacité pour un puzzle
donné mais c'est plutôt son association avec les autres pièces qui se
révèle plus ou moins fertile.
Vous pouvez reconstituer 13 figures convexes avec le Tangram (voir
illustration ci-contre), mais d'autres puzzles de 7 pièces totalisant
16 demi-carrés parviennent à en réaliser davantage sur les 20
théoriquement possibles. le
jeu de Revathi*, Chie-no-ita, Cocogram et Heptex en réalisent
respectivement 15, 16, 16 et 19. D'autres puzzles connus en réalisent
moins que 13 : Pythagoras en reconstitue 12 et Regulus en reconstitue
7 seulement. La forme de certaines pièces empêche, par leur seule
présence, la réalisation de certaines formes convexes. Ainsi, pour le
Tangram, c'est la présence des grands demi-triangles qui empêche la
reconstitution de 4 formes (les formes 2, 5, 8 et 13 selon leur ordre
d'apparition dans le programme). Pythagoras, Regulus et Cocogram sont
eux aussi empéchés de reconstituer ces mêmes formes (2, 5, 8 et 13)
par leur plus encombrante pièce mais restent très différents dans leur
capacité à reconstituer des formes convexes. Ce n'est donc pas la
présence d'une grosse pièce qui révèle cette capacité pour un puzzle
donné mais c'est plutôt son association avec les autres pièces qui se
révèle plus ou moins fertile.
* Le jeu de Revathi est un des 4 puzzles obtenus à l'aide des 7 plus petits polyabolos (il faut enlever un triabolos de la collection des 8 premiers polyabolos pour obtenir un ensemble de 16 demi-carrés). Nous avons dénommé TTPs, TTPr, PPTs et PPTr ces puzzles pour désigner quels triabolos étaient employés (T:Trapèze, P:Pentagone, s:symétrique, r:rien). Ainsi le jeu de Revathi est le puzzle dénommé TTPs qui a les 2 triabolos trapézoïdaux (TT) et le triabolo pentagonal symétrique (Ps). Ces 4 puzzles sont illustrés ci-dessous dans leur capacité à reconstituer le grand carré d'aire 16: seul TTPr ne parvient pas à reconstituer ce carré.

 Le nombre de figures convexes reconstituées par un puzzle va devenir
notre point de mire, notre objectif principal : nous souhaitons trouver
un puzzle capable d'en réaliser le maximum. Si on fait varier le nombre
n de demi-carrés que totalise un puzzle donné, le nombre de figures
convexes théoriquement possibles varie dans le même sens que n mais avec
des irrégularités. Le tableau ci-dessous donne tous les nombres de
formes convexes théoriquement possibles avec une aire de 1 à 20
demi-carrés, plus quelques autres remarquables jusqu'à 100 demi-carrés.
Nous constatons que ce nombre est assez proche du nombre de
demi-triangles (20 pour 16, 38 pour 36, 54 pour 50, etc.). Ce nombre est
plus grand que le nombre de demi-carrés pour toutes les dissections du
carré envisagées sauf pour celles d'aire 18. Nous déduisons de ces
observations que le puzzle cherché - celui qui réalise un maximum de
figures convexes - va probablement avoir une aire supérieure à 16
demi-carrés, afin de bénéficier du grand choix de formes convexes
qu'apporte une grande aire. L'étude des puzzles de grandes aires est
possible avec notre programme mais demande beaucoup de temps de calcul
car alors le choix des tailles de pièces (structure du puzzle) est très
varié et, pour une taille donnée, le choix des pièces possibles est très
grand.
Le nombre de figures convexes reconstituées par un puzzle va devenir
notre point de mire, notre objectif principal : nous souhaitons trouver
un puzzle capable d'en réaliser le maximum. Si on fait varier le nombre
n de demi-carrés que totalise un puzzle donné, le nombre de figures
convexes théoriquement possibles varie dans le même sens que n mais avec
des irrégularités. Le tableau ci-dessous donne tous les nombres de
formes convexes théoriquement possibles avec une aire de 1 à 20
demi-carrés, plus quelques autres remarquables jusqu'à 100 demi-carrés.
Nous constatons que ce nombre est assez proche du nombre de
demi-triangles (20 pour 16, 38 pour 36, 54 pour 50, etc.). Ce nombre est
plus grand que le nombre de demi-carrés pour toutes les dissections du
carré envisagées sauf pour celles d'aire 18. Nous déduisons de ces
observations que le puzzle cherché - celui qui réalise un maximum de
figures convexes - va probablement avoir une aire supérieure à 16
demi-carrés, afin de bénéficier du grand choix de formes convexes
qu'apporte une grande aire. L'étude des puzzles de grandes aires est
possible avec notre programme mais demande beaucoup de temps de calcul
car alors le choix des tailles de pièces (structure du puzzle) est très
varié et, pour une taille donnée, le choix des pièces possibles est très
grand. | nombre de demi-carrés | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ... | 22 | ... | 24 | ... | 28 | ... | 30 | ... | 32 | ... | 36 | ... | 50 | ... | 64 | ... | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dissection du carré | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | ... | 0 | ... | 0 | ... | 0 | ... | 0 | ... | 1 | ... | 1 | ... | 1 | ... | 1 | ... | 1 |
| convexes théoriques | 1 | 3 | 2 | 6 | 3 | 7 | 5 | 11 | 5 | 10 | 6 | 14 | 6 | 9 | 11 | 20 | 9 | 17 | 13 | 22 | ... | 25 | ... | 27 | ... | 31 | ... | 36 | ... | 37 | ... | 38 | ... | 54 | ... | 75 | ... | 123 |
 La constitution du
Tangram utilise des pièces en double : deux petits triangles
(monoabolos) identiques et 2 grands triangles (tetrabolos) identiques.
Cette spécificité du Tangram conduit à une grande similarité de forme
: 5 pièces sur les 7 sont des demi-carrés (triangles isocèles
rectangles) de 3 dimensions différentes. C'est peut-être cette
caractéristique qui contribua à donner au jeu sa popularité. En
faisant ces remarques nous introduisons deux nouveaux paramètres d'un
puzzle : le nombre de pièces en double (2 pour le Tangram) et aussi le
nombre de formes différentes, à un agrandissement près. Ce dernier
paramètre est assez délicat à manier, car certains polyabolos ont les
mêmes angles mais pas les même longueurs... Nous l'avons écarté de
notre étude première, tout en conservant cette possibilité dans le
programme (voir plus loin, réglage de Z).
La constitution du
Tangram utilise des pièces en double : deux petits triangles
(monoabolos) identiques et 2 grands triangles (tetrabolos) identiques.
Cette spécificité du Tangram conduit à une grande similarité de forme
: 5 pièces sur les 7 sont des demi-carrés (triangles isocèles
rectangles) de 3 dimensions différentes. C'est peut-être cette
caractéristique qui contribua à donner au jeu sa popularité. En
faisant ces remarques nous introduisons deux nouveaux paramètres d'un
puzzle : le nombre de pièces en double (2 pour le Tangram) et aussi le
nombre de formes différentes, à un agrandissement près. Ce dernier
paramètre est assez délicat à manier, car certains polyabolos ont les
mêmes angles mais pas les même longueurs... Nous l'avons écarté de
notre étude première, tout en conservant cette possibilité dans le
programme (voir plus loin, réglage de Z).
Le nombre de doubles est plus facile à prendre en compte, et surtout, il influence grandement la capacité de reconstitution des formes convexes d'un puzzle. En effet, il est assez facile de trouver des puzzles capables de reconstituer beaucoup de formes convexes si on s'autorise à utiliser des doubles. Avec 7 pièces totalisant 16 demi-carrés, lorsqu'on utilise 5 doubles - 5 doubles est alors le maximum possible de doubles - on peut reconstituer jusqu'à 15 formes convexes. Avec 4 doubles on peut en reconstituer 18, avec 2 ou 3 doubles on peut en reconstituer jusqu'à 19 (Heptex en fait partie car il a 7 pièces dont 2 doubles). Avec 1 double on ne dépasse pas 16 et sans aucun double (le jeu de Revathi, aussi appelé TTPs est le meilleur de cet ensemble de 4 puzzles) on arrive à peine à 15 formes convexes. Pour résumer cette première approche : afin de réaliser le maximum de formes convexes il faut un peu de doubles mais pas trop.
Si on continue à faire varier le nombre de doubles tout en jouant sur le nombre de pièces du puzzle, on peut penser qu'on arrivera peut-être à reconstituer les 20 formes convexes théoriquement possibles. Nous avons essayé* en prenant de 5 à 10 pièces et entre 0 à 8 doubles, sans trouver de puzzle reconstituant les 20 formes convexes (le tableau ci-dessous donne les résultats de cette recherche). Lorsque la forme la plus étroite (forme n°8) est réalisable, le jeu de pièces est tellement particulier qu'il ne peut reconstituer les autres formes convexes. Par exemple, un ensemble de 8 parallélogrammes (puzzle ayant 8 pièces dont 7 doubles) reconstitue 4 formes convexes seulement, dont la forme n°8 bien entendu. Si on poursuit cette étude avec plus de pièces, on arrivera bien à des puzzles pouvant reconstituer les 20 formes convexes mais ce gain se fera au détriment d'une dégradation de la qualité esthétique du puzzle (trop de pièces semblables). La plus simple des preuves, le puzzle constitué de 16 demi-triangles d'aire 1 qui a donc 15 doubles, parvient à ce but de toute évidence mais peut-on parler à son propos d'un puzzle? Si l'on joue avec le Tangram plutôt qu'avec 16 petits triangles identiques, c'est parce que cet assemblage de 7 pièces a des qualités esthétiques particulières dont la première est un nombre réduit de pièces. Nous retiendrons ici qu'il va toujours nous falloir considérer le nombre de pièces d'un puzzle parallèlement à sa capacité de reconstitution des formes convexes.
* Cette exploration de la capacité des différents puzzles à
reconstituer les formes convexes est assez rapide à effectuer pour 16
triangles à l'aide de notre programme. Il y a tout de même 265 740
puzzles à essayer (156 465 à 5 pièces, 67 520 à 6 pièces, 27 248 à 7
pièces, 9 900 à 8 pièces, 3 451 à 9 pièces, 1 156 à 10 pièces), avec
pour chacun 20 formes à reconstituer. Ces nombres, calculés par le
programme, sont dépendants du choix de pièces à disposition, et comme,
pour simplifier le choix, nous n'avons pas mis tous les polyabolos de
taille supérieure à 5, ces nombres sont sous-estimés par rapport à la
réalité. En effet, pour totaliser 16 triangles avec 5 pièces et 0
double, par exemple, la première structure qui est proposée est
"12229", ce qui signifie 1 monoabolo, 3 diabolos et un 9-abolo. Il n'y
a que 3 choix dans le programme pour le 9-abolo qui doit être choisi,
alors que dans la réalité, il en existe 3667.. Nous n'avons conservé
que quelques polyabolos de grandes tailles, convexes et pas trop
allongés, au détriment d'une exhaustivité qui aurait vite étouffée nos
recherches. Si l'on veut supprimer les limites que nous nous sommes
imposées et offrir une possibilité de choix exhaustif, il faudrait
sans doute réécrire le programme en utilisant des algorithmes et un
langage plus performants (nous avons utilisé le langage java qui n'est
pas le plus performant pour les calculs et nos algorithmes sont ceux
d'un amateur..) sinon les recherches seront extrèmement longues, même
pour 16 triangles.
| nombre de doubles | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| puzzles à 5 pièces | 15 | 15 | 14 | 14 | no | no | no | no | no |
| puzzles à 6 pièces | 16 | 16 | 17 | 16 | 16 | no | no | no | no |
| puzzles à 7 pièces | 15 | 16 | 19 | 19 | 18 | 15 | no | no | no |
| puzzles à 8 pièces | no | no | 16 | 19 | 19 | 19 | 18 | 4 | no |
| puzzles à 9 pièces | no | no | no | 16 | 19 | 19 | 19 | 18 | no |
| puzzles à 10 pièces | no | no | no | no | no | no | 19 | 19 | 19 |
| puzzles à 11 pièces | no | no | no | no | no | no | no | no | |
Nous voudrions pouvoir mesurer la valeur d'un puzzle en additionnant ou soustrayant des entiers : les paramètres s'additionnant sont ceux qui augmentent la valeur du puzzle comme le nombre de formes convexes reconstituables, les paramètres à soustraire sont ceux qui en diminue la valeur comme le nombre de pièces. Nous avons considéré que le nombre de pièces diminue la valeur d'un jeu ainsi que le nombre de doubles, d'après les observations ci-dessus. Quant aux paramètres qui en augmente la valeur, nous avons ajouté la capacité de reconstituer le carré (même si elle est déjà comptée un fois dans les formes convexes) car on préfère les dissections du carré. Nous avons aussi ajouté des paramètres mesurant la diversité des formes des pièces : le nombre d'angles différents (au choix parmi 45, 90, 135, 225, 270 et 315°) et le nombre de longueurs différentes dans le sens du quadrillage ou dans le sens diagonal. Ce choix s'oppose à celui qui considère que la simplicité des formes du Tangram (nombre de formes différentes) ajoutait de la valeur à ce jeu. Notre choix est plutôt guidé par une reconnaissance de la difficulté d'un jeu - difficulté venant de la diversité des formes - comme valeur positive.
Notre idée est de fabriquer un indice composite subjectif qui mesure au mieux la valeur que l'on veut attribuer aux puzzles pour les comparer entre eux afin d'en déterminer un meilleur que les autres. Nous avons donc construit ce premier indice, baptisé score Z, qu'il est facile de calculer pour tout puzzle de la famille du Tangram. La formule pour le score est Z = L + A - P - D + F + C, où :
- L est le nombre de longueurs différentes
- A est le nombre d'angles différents
- P est le nombre de pièces du puzzle
- D est le nombre de pièces en double
- F est le nombre de figures convexes réalisables avec le puzzle
- C est la possibilité de reconstituer le carré (1 si oui, 0 sinon)
Le nombre F de figures convexes qu'il est possible de reconstituer
est le plus difficile à obtenir car, sans ordinateur, il est déjà
assez long d'essayer toutes les formes convexes pour un seul puzzle.
Comme il s'agit de recommencer avec tous les puzzles possibles, cela
est impossible de tout vérifier à la main, même si ce jeu peut occuper
agréablement quelques soirées. Nous avons utilisé un programme : le
programme d'Eric Wharshop (wintanxx) qui fonctionne très bien pour les
puzzles d'aire 16 triangles et qui accepte jusqu'à 20 triangles et 8
pièces. Nous avons commencé à accumuler des résultats grâce à ce
programme qu'Eric avait l'amabilité de modifier à notre demande pour
le rendre plus performant et riche d'utilisation. Mais assez vite il
apparu que les limitations du programme d'Eric nous empêchait de voir
au-delà de 20 triangles, au-delà de 8 pièces et aussi au delà de
pièces incluses dans des carrés 2x2... Il nous fallut développer notre
propre programme, qui s'est avéré assez éloigné de celui d'Eric. Les
limitations avaient été repoussées bien loin, mais nous avions perdu
en rapidité (nos procédures en Java ne rivalisent pas avec celles du
langage C utilisé par Eric). Mais il ne nous fallait pas de
limitations pour explorer le domaine aussi largement que nécessaire.
Pour diminuer le temps de traitement nous avons trouvé quelques
astuces, et maintenant, globalement cela fonctionne correctement.
 Les puzzles connus ou ceux
que nous avons été amené à nommer sont les premiers candidats au
classement opéré par le score Z. Le tableau suivant nous donne le
détail du calcul de Z pour ces puzzles. Si le jeu de Revathi et Heptex
sont parmi ceux qui totalisent un bon score Z (Z=17 pour ces 2
puzzles), le Tangram n'obtient qu'un médiocre Z=12... L'utilisation
d'un ordinateur nous a permis d'identifier rapidement 8 autres puzzles
d'aire 16 triangles qui ont le score Z le plus élevé : Z=19. Ces
puzzles ont été dénommés TAO1 à TAO8 pour rappeler l'utilisation de
l'informatique pour leur découverte (TAO étant l'acronyme de Tangrams
Assistés par Ordinateur). A ce moment de notre histoire, seul le
programme d'Eric existait, aussi nous avons essayé toutes les
possibilités (presque toutes) offertes par ce programme pour tenter de
battre ce record. Parmi les puzzles de moins de 20 triangles d'aire et
de 8 pièces au plus, il n'en était pas un seul qui dépasse ce score
Z=19.
Les puzzles connus ou ceux
que nous avons été amené à nommer sont les premiers candidats au
classement opéré par le score Z. Le tableau suivant nous donne le
détail du calcul de Z pour ces puzzles. Si le jeu de Revathi et Heptex
sont parmi ceux qui totalisent un bon score Z (Z=17 pour ces 2
puzzles), le Tangram n'obtient qu'un médiocre Z=12... L'utilisation
d'un ordinateur nous a permis d'identifier rapidement 8 autres puzzles
d'aire 16 triangles qui ont le score Z le plus élevé : Z=19. Ces
puzzles ont été dénommés TAO1 à TAO8 pour rappeler l'utilisation de
l'informatique pour leur découverte (TAO étant l'acronyme de Tangrams
Assistés par Ordinateur). A ce moment de notre histoire, seul le
programme d'Eric existait, aussi nous avons essayé toutes les
possibilités (presque toutes) offertes par ce programme pour tenter de
battre ce record. Parmi les puzzles de moins de 20 triangles d'aire et
de 8 pièces au plus, il n'en était pas un seul qui dépasse ce score
Z=19.
| Nom Puzzle | N° Pièces | L | A | P | D | F | C | Z |
|---|---|---|---|---|---|---|---|---|
| Tangram | 1 1 2 3 4 9 9 | 4 | 3 | 7 | 2 | 13 | 1 | 12 |
| Pythagoras | 1 1 2 2 4 11 13 | 3 | 3 | 7 | 2 | 12 | 1 | 10 |
| Chie-no-ita | 1 2 2 3 4 5 10 | 4 | 3 | 7 | 1 | 16 | 1 | 16 |
| Heptex | 1 2 2 3 3 5 11 | 3 | 3 | 7 | 2 | 19 | 1 | 17 |
| TTPS (Revathi) | 1 2 3 4 5 6 7 | 4 | 4 | 7 | 0 | 15 | 1 | 17 |
| TTPr | 1 2 3 4 5 6 8 | 4 | 4 | 7 | 0 | 12 | 0 | 13 |
| TAO5 | 1 2 5 6 7 9 | 4 | 4 | 6 | 0 | 16 | 1 | 19 |
 Une des fonctionnalités
existante du programme d'Eric était de rechercher toutes les figures
symétriques ayant un certain nombre de côtés. On peut procéder avec
ces formes trouvées comme avec les formes convexes : essayer de les
reconstituer avec des puzzles. Les figures symétriques (le programme
d'Eric ne distingue pas les figures ayant un axe ou un centre de
symétrie) sont très nombreuses, beaucoup plus nombreuses que les
figures convexes. Le tableau ci-dessous donne une idée de ce que l'on
obtient pour des puzzles d'aire 16 triangles. Lorsqu'on augmente le
nombre de côtés, les quantités deviennent tellement grandes qu'elles
dépassent nettement les capacités du programme d'Eric (255 éléments)
et nécessitent de fractionner la recherche. Il aurait fallu une vraie
logistique et un partage du travail pour en venir à bout.
Une des fonctionnalités
existante du programme d'Eric était de rechercher toutes les figures
symétriques ayant un certain nombre de côtés. On peut procéder avec
ces formes trouvées comme avec les formes convexes : essayer de les
reconstituer avec des puzzles. Les figures symétriques (le programme
d'Eric ne distingue pas les figures ayant un axe ou un centre de
symétrie) sont très nombreuses, beaucoup plus nombreuses que les
figures convexes. Le tableau ci-dessous donne une idée de ce que l'on
obtient pour des puzzles d'aire 16 triangles. Lorsqu'on augmente le
nombre de côtés, les quantités deviennent tellement grandes qu'elles
dépassent nettement les capacités du programme d'Eric (255 éléments)
et nécessitent de fractionner la recherche. Il aurait fallu une vraie
logistique et un partage du travail pour en venir à bout.
Pour leur capacité à réaliser des figures symétriques, on remarque des puzzles qui ne se font pas remarquer autrement, comme ce puzzle n°760 (avec nos références, il est constitué des pièces 1 2 3 5 8 23) qui est le champion de sa catégorie (6 pièces de taille inférieures ou égales à 5 triangles). Ce puzzle est capable de reconstituer 1400 figures symétriques ayant de 3 à 12 côtés. Au cours de notre recherche, nous n'avons trouvé que 2 puzzles qui dépassent cette valeur : Heptex (1488 figures) et TTPr (1639 figures symétriques). Il est étonnant de remarquer que 760 et TTPr sont excellents pour reconstituer des figures symétriques alors qu'ils étaient moyens pour les figures convexes (Z=17 pour 760 et 12 pour TTPr). De plus, ces deux puzzles ne parviennent pas à reconstituer le carré!
Avec notre programme, nous avons voulu pouvoir distinguer les formes ayant un centre de symétrie de celles qui ont un axe. Nous pouvons par exemple, comparer les puzzles connus pour leur capacité à reconstituer les 136 formes ayant un centre de symétrie et 3 à 8 côtés : Le meilleur est Heptex (101) suivi de n° 760 (78),Chie-no-ita (72), TTPr (70), TTPs (61), Tangram (58), TAO5 (38), Penta (33) et Pythagoras (29).
 La capacité à
reconstituer des formes symétriques est difficile à intégrer au calcul
du score Z vu ces nombres qui ne sont pas du même ordre de grandeur que
les autres paramètres. Comme Eric l'a suggéré, on pourrait considérer
les pourcentages obtenus, mais alors se pose la question de savoir quel
pourcentage utiliser. Les pièces du Tangram parviennent à reconstituer 8
figures symétriques à 18 côtés (voir illustration) sur les 1515
théoriquement possibles avec 16 demi-carrés. Ce résultat est-il
exploitable sous la forme d'un pourcentage (16/1515x100=1% environ) et
n'a t'il pas moins d'importance que le pourcentage obtenu pour
l'ensemble des figures symétriques? Les temps de calcul pour trouver
toutes les formes symétriques deviennent rapidement très grands, s'il
faut ensuite essayer pour chaque puzzle toutes les formes symétriques
possibles, la recherche devient interminable. Nous avons fini par
conclure que la capacité à reconstituer des formes symétriques ne
pouvait pas être prise en compte simplement par notre étude aussi
laissons nous de côté ce paramètre pour la suite.
La capacité à
reconstituer des formes symétriques est difficile à intégrer au calcul
du score Z vu ces nombres qui ne sont pas du même ordre de grandeur que
les autres paramètres. Comme Eric l'a suggéré, on pourrait considérer
les pourcentages obtenus, mais alors se pose la question de savoir quel
pourcentage utiliser. Les pièces du Tangram parviennent à reconstituer 8
figures symétriques à 18 côtés (voir illustration) sur les 1515
théoriquement possibles avec 16 demi-carrés. Ce résultat est-il
exploitable sous la forme d'un pourcentage (16/1515x100=1% environ) et
n'a t'il pas moins d'importance que le pourcentage obtenu pour
l'ensemble des figures symétriques? Les temps de calcul pour trouver
toutes les formes symétriques deviennent rapidement très grands, s'il
faut ensuite essayer pour chaque puzzle toutes les formes symétriques
possibles, la recherche devient interminable. Nous avons fini par
conclure que la capacité à reconstituer des formes symétriques ne
pouvait pas être prise en compte simplement par notre étude aussi
laissons nous de côté ce paramètre pour la suite.
| Nombre de côtés | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Figures convexes | 1 | 13 | 2 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Figures symétriques | 1 | 11 | 2 | 35 | 11 | 206 | 71 | 654 | 214 | 1708 | 377 | 2914 | 443 | 3249 | 239 | 1515 |
| Figures totales | 1 | 13 | 31 | 325 | 1982 | 10902 | 46980 | 150000* | 260000* | 410000* | 600000* | 850000* | 1100000* | 1300000* | 1200000* | 960587 |
 Notre programme a
été développé pour essayer d'explorer une partie inaccessible au
programme d'Eric : les puzzles d'aire supérieure à 20 triangles. Cette
caractéristique a permis de pulveriser facilement les records pour
l'indice Z : nous avons essayé avec des puzzles d'aire 32 triangles
(37 formes convexes réalisables) et nous avons rapidement obtenu des Z
égaux à 35! Nous avons ensuite essayé avec 36 triangles, puis 50 et
enfin 64. Avec des puzzles d'aire 36 triangles (38 formes convexes
réalisables) nous n'avons tout d'abord pas trouvé mieux que Z=35. Avec
50 triangles on atteint assez facilement Z=49 et avec 64 triangles, un
puzzle au moins atteint Z=60! C'est assez difficile d'améliorer ces
résultats car les combinaisons de pièces sont extêmement nombreuses.
Notre programme a
été développé pour essayer d'explorer une partie inaccessible au
programme d'Eric : les puzzles d'aire supérieure à 20 triangles. Cette
caractéristique a permis de pulveriser facilement les records pour
l'indice Z : nous avons essayé avec des puzzles d'aire 32 triangles
(37 formes convexes réalisables) et nous avons rapidement obtenu des Z
égaux à 35! Nous avons ensuite essayé avec 36 triangles, puis 50 et
enfin 64. Avec des puzzles d'aire 36 triangles (38 formes convexes
réalisables) nous n'avons tout d'abord pas trouvé mieux que Z=35. Avec
50 triangles on atteint assez facilement Z=49 et avec 64 triangles, un
puzzle au moins atteint Z=60! C'est assez difficile d'améliorer ces
résultats car les combinaisons de pièces sont extêmement nombreuses.
 Pour donner un exemple, nous
avons essayé de battre le record Z=35 parmi les puzzles d'aire 36
triangles, au sein de la structure 1-2-3-4-5-6-7-8 qui contient pas
moins de 17.256.960 puzzles (avec les omissions déjà mentionnées).
Cette recherche a été poursuivie pendant 50 h avant de trouver un
vainqueur : le n°87.564 constitué des 8 pièces 1.2.6.9.48.114.161.167
obtient Z=36! Par la suite, nous avons mis en place une procédure
d'optimisation qui consiste à essayer d'abord les formes les plus
longues pour éliminer le plus tôt possible les puzzles qui ne pourront
pas battre le record. Nous avons été bien inspiré car la même
recherche ne prend plus maintenant que 45 minutes! Nous en avons
profité pour ajouter un répis de 10 s tous les 1000 puzzles examinés
pour ménager l'ordinateur...
Pour donner un exemple, nous
avons essayé de battre le record Z=35 parmi les puzzles d'aire 36
triangles, au sein de la structure 1-2-3-4-5-6-7-8 qui contient pas
moins de 17.256.960 puzzles (avec les omissions déjà mentionnées).
Cette recherche a été poursuivie pendant 50 h avant de trouver un
vainqueur : le n°87.564 constitué des 8 pièces 1.2.6.9.48.114.161.167
obtient Z=36! Par la suite, nous avons mis en place une procédure
d'optimisation qui consiste à essayer d'abord les formes les plus
longues pour éliminer le plus tôt possible les puzzles qui ne pourront
pas battre le record. Nous avons été bien inspiré car la même
recherche ne prend plus maintenant que 45 minutes! Nous en avons
profité pour ajouter un répis de 10 s tous les 1000 puzzles examinés
pour ménager l'ordinateur...
 Tant que nous ne
pouvions aller au delà de 20 triangles nous croyions que z était
limité à 19. Maintenant que nous avons atteint l'indice Z=60 avec les
puzzles d'aire 64, nous avons tendance à penser que l'indice Z n'est
pas limité. Il semble évident que le nombre de formes convexes
réalisables devient aussi grand que l'on veut lorsque le nombre de
triangles augmente (approximativement la valeur du nombre de
triangles). Il semble par conséquent raisonnable de penser qu'on peut
sans doute dépasser n'importe quelle valeur de Z, car si on augmente
un peu le nombre de pièces, on parvient à reconstituer d'un coup
beaucoup plus de formes convexes.
Tant que nous ne
pouvions aller au delà de 20 triangles nous croyions que z était
limité à 19. Maintenant que nous avons atteint l'indice Z=60 avec les
puzzles d'aire 64, nous avons tendance à penser que l'indice Z n'est
pas limité. Il semble évident que le nombre de formes convexes
réalisables devient aussi grand que l'on veut lorsque le nombre de
triangles augmente (approximativement la valeur du nombre de
triangles). Il semble par conséquent raisonnable de penser qu'on peut
sans doute dépasser n'importe quelle valeur de Z, car si on augmente
un peu le nombre de pièces, on parvient à reconstituer d'un coup
beaucoup plus de formes convexes.
Un gros obstacle aux vérifications expérimentales de ces hypothèses
est la limite imposée par le temps de calcul : nous n'avons pas encore
réussi à obtenir la performance d'un puzzle ayant une aire de 100
triangles. Nous avons mis un puzzle de 12 pièces baptisé hectoTangram
dans les puzzles connus, mais à chaque fois qu'on l'a essayé, le
programme n'arrive pas à la fin du traitement... Il faut dire que 12
pièces augmentent considérablement la durée de l'algorithme de
recherche des solutions, et comme il y a, à chaque fois, 123 formes
convexes à tester, cela fait beaucoup.
Les puzzles qui obtiennent les meilleurs score Z avec une aire
importante (supérieure ou égale à 32) sont constitués de 8, 9 ou 10
pièces. Ce nombre étant plus important que le nombre de pièces du
Tangram, nous obtenons des puzzles vraiment plus compliqués, plus
difficiles, sans forcément y mettre d'autres valeurs. Pourtant nous
pensons qu'il doit y avoir une beauté dans un puzzle et certainement
ces puzzles qui réussissent mieux seraient vraiment plus beaux s'ils
étaient fait de 7 pièces comme le Tangram, ou même moins. L'idée qui
ressort de cette remarque est qu'il faudrait utiliser un score Z qui
pénalise davantage les scores ayant un grand nombre de pièces.
Supprimer seulement un point de score par pièce comme le fait notre
indice Z actuel condamne les puzzles de petite aire à être les
derniers si on considère de la même façon le nombre de pièces et le
nombre de formes convexes reconstituées. Afin de corriger ce défaut du
score Z, nous proposons un indice équilibré, que nous baptisons score
X, calculé comme suit X = L + A + P(7 - P) - D + F + C. Le seul
changement par rapport à Z est le terme P(7-P) qui se substitue à -P.
Les gains obtenus par pièces sont donnés dans le tableau suivant.
| Nombre de pièces | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|
| Gain à ajouter à Z | 16 | 15 | 12 | 7 | 0 | -9 | -20 | -33 | -48 |
Que donnent les puzzles connus pour ce nouvel indice X? Quelque chose
de beaucoup plus homogène. Les puzzles ayant peu de pièces sont
avantagés, ceux qui en ont beaucoup sont désavantagés, l'équilibre
étant sur 7 pièces (pour 7 pièces le terme P(7-P) est nul et maximum,
pour toute autre valeur de P ce terme est négatif). Par exemple un
puzzle de 12 pièces perd 48 points de score tandis qu'un puzzle de 4
pièces en gagne 16. Cela va changer considérablement les résultats.
Voyons plutôt :
| Nom Puzzle | P | score Z | score X |
|---|---|---|---|
| Tangram | 7 | 12 | 19 |
| Pythagoras | 7 | 10 | 17 |
| Chie-no-ita | 7 | 16 | 23 |
| Heptex | 7 | 17 | 24 |
| TTPS (Revathi) | 7 | 17 | 24 |
| TTPr | 7 | 13 | 20 |
| TAO5 | 6 | 19 | 31 |
| 32T:WinZ35 | 9 | 35 | 17 |
| 36T:WinZ36 | 8 | 36 | 36 |
| 50T:WinZ49 | 10 | 49 | 29 |
| 64T:WinZ60 | 10 | 60 | 40 |
 Si, pour ce nouvel
indice X, les puzzles d'aire 16 semblent avoir déjà tout donné et ne
devrait pas dépasser beaucoup le score X=31 des TAO (une vérification
s'impose quand même, notamment du côté des puzzles de 4 ou 5 pièces),
pour les puzzles de grande aire, il va falloir explorer les
assemblages de 6 ou 7 pièces, l'équilibrage semblant donner des
chances mieux réparties et plus imprévisibles quant à la suprématie
des puzzles de grande aire. En examinant les puzzles d'aire 16 ayant
de 2 à 5 pièces, nous trouvons un meilleur score X que celui des TAO:
le puzzle à 5 pièces "Penta" obtient X=33 pour 15 formes convexes
reconstituables.
Si, pour ce nouvel
indice X, les puzzles d'aire 16 semblent avoir déjà tout donné et ne
devrait pas dépasser beaucoup le score X=31 des TAO (une vérification
s'impose quand même, notamment du côté des puzzles de 4 ou 5 pièces),
pour les puzzles de grande aire, il va falloir explorer les
assemblages de 6 ou 7 pièces, l'équilibrage semblant donner des
chances mieux réparties et plus imprévisibles quant à la suprématie
des puzzles de grande aire. En examinant les puzzles d'aire 16 ayant
de 2 à 5 pièces, nous trouvons un meilleur score X que celui des TAO:
le puzzle à 5 pièces "Penta" obtient X=33 pour 15 formes convexes
reconstituables.
 Parmi les quelques essais
sporadiques que j'ai pu effectué à ce jour pour les puzzles de grande
taille, j'ai tout d'abord trouvé un puzzle de 7 pièces et 36 triangles
dans la structure 1.2.4.5.7.8.9 (pièces n° 1.2.9.26.161.167.174) qui
obtient le meilleur score X avec X=42. Comme il a déjà été dit, pour
les grandes aires c'est difficile de faire autre chose que des essais
sporadiques, et pour s'approcher du maximum un peu de reflexion va
nous aider, car il ne sert à rien de chercher dans certaines
structures, là où des pièces seraient trop encombrantes pour obtenir
un bon score. Nous avons ensuite trouvé plusieurs puzzles de 6 pièces
et 32 triangles (le premier dans la structure 1.3.5.7.8) qui
obtiennent un meilleur score X avec X=43. Il est problable qu'en
cherchant davantage nous trouverons un puzzle ayant un meilleur score
X que 43, mais rien ne permet de penser que le score X, comme le score
Z, est illimité. Si on augmente la taille du puzzle, le nombre de
formes convexes théoriques augmente sans limite, mais le paramètre
P(7-P) restreint nécessairement le nombre de pièces ce qui n'est pas
favorable aux puzzles de grande taille. Le défi est donc ouvert de
trouver le puzzle ayant le meilleur score X ou bien de montrer que ce
score X est illimité (ce que nous ne pensons pas).
Parmi les quelques essais
sporadiques que j'ai pu effectué à ce jour pour les puzzles de grande
taille, j'ai tout d'abord trouvé un puzzle de 7 pièces et 36 triangles
dans la structure 1.2.4.5.7.8.9 (pièces n° 1.2.9.26.161.167.174) qui
obtient le meilleur score X avec X=42. Comme il a déjà été dit, pour
les grandes aires c'est difficile de faire autre chose que des essais
sporadiques, et pour s'approcher du maximum un peu de reflexion va
nous aider, car il ne sert à rien de chercher dans certaines
structures, là où des pièces seraient trop encombrantes pour obtenir
un bon score. Nous avons ensuite trouvé plusieurs puzzles de 6 pièces
et 32 triangles (le premier dans la structure 1.3.5.7.8) qui
obtiennent un meilleur score X avec X=43. Il est problable qu'en
cherchant davantage nous trouverons un puzzle ayant un meilleur score
X que 43, mais rien ne permet de penser que le score X, comme le score
Z, est illimité. Si on augmente la taille du puzzle, le nombre de
formes convexes théoriques augmente sans limite, mais le paramètre
P(7-P) restreint nécessairement le nombre de pièces ce qui n'est pas
favorable aux puzzles de grande taille. Le défi est donc ouvert de
trouver le puzzle ayant le meilleur score X ou bien de montrer que ce
score X est illimité (ce que nous ne pensons pas).
 Le choix arbitraire des
paramètres entrant dans le calcul de ces indices composites Z et X
peut sembler bien contestable. Pour cette raison, nous avons orienté
nos recherches vers la simplification: puisqu'il est clair que le
nombre de pièces doit être limité et que nous cherchons spécifiquement
des dissections du carré, essayons de déterminer, pour un nombre de
pièces donné, la dissection du carré qui reconstitue le maximum de
formes convexes. De cette façon nous disqualifions les puzzles de
grande aire pour des nombres de pièces pas trop élevé, mais nous leur
rendons leur prépondérance en augmentant le nombre de pièces. Cette
approche a le mérite d'être plus simple à énoncer et plus objective,
et donc plus facile à justifier vis-à-vis d'un tiers. Elle peut aussi
atteindre l'exhaustivité pour des nombres de pièces pas trop grand.
Par exemple, pour des dissections à 2 pièces, on trouve 3 formes
convexes avec le seul puzzle d'aire 2 existant, et on ne trouve pas
mieux avec les puzzles d'aire supérieure à 2. Le puzzle trouvé a un
double mais on ne comptabilise pas cela ici. On ne comptabilise pas
non plus la diversité des longueurs ou des angles. La réussite du
carré n'est plus ici comptabilisée (on ne compte que les formes
convexes) mais elle est obligatoire puisqu'on disqualifie d'office les
puzzles n'étant pas une dissection du carré.
Le choix arbitraire des
paramètres entrant dans le calcul de ces indices composites Z et X
peut sembler bien contestable. Pour cette raison, nous avons orienté
nos recherches vers la simplification: puisqu'il est clair que le
nombre de pièces doit être limité et que nous cherchons spécifiquement
des dissections du carré, essayons de déterminer, pour un nombre de
pièces donné, la dissection du carré qui reconstitue le maximum de
formes convexes. De cette façon nous disqualifions les puzzles de
grande aire pour des nombres de pièces pas trop élevé, mais nous leur
rendons leur prépondérance en augmentant le nombre de pièces. Cette
approche a le mérite d'être plus simple à énoncer et plus objective,
et donc plus facile à justifier vis-à-vis d'un tiers. Elle peut aussi
atteindre l'exhaustivité pour des nombres de pièces pas trop grand.
Par exemple, pour des dissections à 2 pièces, on trouve 3 formes
convexes avec le seul puzzle d'aire 2 existant, et on ne trouve pas
mieux avec les puzzles d'aire supérieure à 2. Le puzzle trouvé a un
double mais on ne comptabilise pas cela ici. On ne comptabilise pas
non plus la diversité des longueurs ou des angles. La réussite du
carré n'est plus ici comptabilisée (on ne compte que les formes
convexes) mais elle est obligatoire puisqu'on disqualifie d'office les
puzzles n'étant pas une dissection du carré.
 En procédant ainsi, on règle
rapidement le compte des dissections comptant peu de pièces. Pour des
dissections à 3 pièces, on trouve 7 formes convexes au maximum avec un
puzzle d'aire 8 qui a un double. Pour des dissections à 4 pièces, on
trouve 10 formes convexes au maximum avec un puzzle d'aire 8 aussi qui
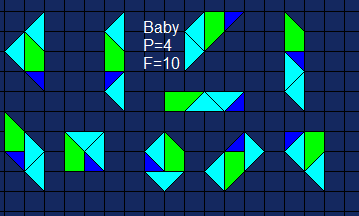
a un double et que nous avons appelé "Baby". Pour des dissections à 5
pièces, on entre dans le domaine de compétence des puzzles d'aire 16
et on retrouve les 15 formes convexes du puzzle "Penta", déjà cité
pour sa meilleure performance au score X.
En procédant ainsi, on règle
rapidement le compte des dissections comptant peu de pièces. Pour des
dissections à 3 pièces, on trouve 7 formes convexes au maximum avec un
puzzle d'aire 8 qui a un double. Pour des dissections à 4 pièces, on
trouve 10 formes convexes au maximum avec un puzzle d'aire 8 aussi qui
a un double et que nous avons appelé "Baby". Pour des dissections à 5
pièces, on entre dans le domaine de compétence des puzzles d'aire 16
et on retrouve les 15 formes convexes du puzzle "Penta", déjà cité
pour sa meilleure performance au score X.
 Pour des dissections à 6
pièces, on sort déjà du domaine de compétence des puzzles d'aire 16
pour entrer dans celle des puzzles d'aire 32. Nous avons trouvé une
dissection du carré d'aire 32 qui réussit à reconstituer 24 formes
convexes, mais est-ce la meilleure? C'est déjà plus difficile ici de
viser l'exhaustivité puisque nous devons envisager de très nombreuses
structures ayant chacune de très nombreuses façons d'être réalisées.
Nous sommes gênés aussi par une limitation de notre programme qui ne
permet pas d'utiliser des pièces d'aire supérieure à 10.
Pour des dissections à 6
pièces, on sort déjà du domaine de compétence des puzzles d'aire 16
pour entrer dans celle des puzzles d'aire 32. Nous avons trouvé une
dissection du carré d'aire 32 qui réussit à reconstituer 24 formes
convexes, mais est-ce la meilleure? C'est déjà plus difficile ici de
viser l'exhaustivité puisque nous devons envisager de très nombreuses
structures ayant chacune de très nombreuses façons d'être réalisées.
Nous sommes gênés aussi par une limitation de notre programme qui ne
permet pas d'utiliser des pièces d'aire supérieure à 10.
 Pour des dissections à 7
pièces, nous ne pouvons faire mieux que des tentatives ponctuelles
mais il semblerait que nous sortions du domaine de compétence des
puzzles d'aire 32 pour entrer dans celle des puzzles d'aire 36. Le
mieux que nous ayons trouvé est une dissection d'aire 36 qui réussit à
reconstituer 31 formes convexes alors que parmi les dissections d'aire
32 nous n'avons pas trouvé mieux que ce puzzle reconstituant 30 formes
convexes. Nous ne sommes pas allé beaucoup plus loin dans cette
exploration à cause des limites imposées par notre programme. Pour les
dissections à 8 et 9 pièces, nous avons jeté un oeil parmi les puzzles
d'aire 50 et en avons trouvé un de 8 pièces reconstituant 40 formes
convexes et un de 9 pièces en reconstituant 47. Même si rien ne permet
d'affirmer que ce sont des maxima, nous ne sommes pas loin des 54
formes convexes théoriquement reconstituables avec des puzzles de
cette taille. La véritable question est alors de savoir si, avec des
puzzles d'aire 64 (75 formes convexes théoriques) ou 100 (123 formes
convexes théoriques), nous ne pourrions faire mieux. Nous comprenons
bien que notre investigation doit s'arrêter faute de moyens appropriés
pour la pousser plus loin.
Pour des dissections à 7
pièces, nous ne pouvons faire mieux que des tentatives ponctuelles
mais il semblerait que nous sortions du domaine de compétence des
puzzles d'aire 32 pour entrer dans celle des puzzles d'aire 36. Le
mieux que nous ayons trouvé est une dissection d'aire 36 qui réussit à
reconstituer 31 formes convexes alors que parmi les dissections d'aire
32 nous n'avons pas trouvé mieux que ce puzzle reconstituant 30 formes
convexes. Nous ne sommes pas allé beaucoup plus loin dans cette
exploration à cause des limites imposées par notre programme. Pour les
dissections à 8 et 9 pièces, nous avons jeté un oeil parmi les puzzles
d'aire 50 et en avons trouvé un de 8 pièces reconstituant 40 formes
convexes et un de 9 pièces en reconstituant 47. Même si rien ne permet
d'affirmer que ce sont des maxima, nous ne sommes pas loin des 54
formes convexes théoriquement reconstituables avec des puzzles de
cette taille. La véritable question est alors de savoir si, avec des
puzzles d'aire 64 (75 formes convexes théoriques) ou 100 (123 formes
convexes théoriques), nous ne pourrions faire mieux. Nous comprenons
bien que notre investigation doit s'arrêter faute de moyens appropriés
pour la pousser plus loin.
 Pour résumer ces
derniers résultats, nous avons reporté les maxima obtenus pour chaque
valeur de P, le nombre de pièces du puzzle, et nous obtenons cette
courbe d'allure exponentielle. Nous avons prolongé en extrapolant de
façon approximative les morceaux de cette courbe, comme s'ils étaient
des portions des courbes donnant, pour une aire donnée, le nombre de
formes convexes selon le nombre de pièces. De cette manière nous
voyons que nos résultats apparaissent comme l'enveloppe de ces
différentes courbes qui ont chacune par nécessité, vocation à
atteindre la limite fixée par le nombre de formes convexes théoriques.
Pour résumer ces
derniers résultats, nous avons reporté les maxima obtenus pour chaque
valeur de P, le nombre de pièces du puzzle, et nous obtenons cette
courbe d'allure exponentielle. Nous avons prolongé en extrapolant de
façon approximative les morceaux de cette courbe, comme s'ils étaient
des portions des courbes donnant, pour une aire donnée, le nombre de
formes convexes selon le nombre de pièces. De cette manière nous
voyons que nos résultats apparaissent comme l'enveloppe de ces
différentes courbes qui ont chacune par nécessité, vocation à
atteindre la limite fixée par le nombre de formes convexes théoriques.
En guise de conclusion : les dissections du carré d'aire 16 sont les plus représentées parmi les puzzles historiques de la famille du Tangram. Pourtant celles-ci ne parviennent à surpasser les autres dissection du carré, dans leur capacité à reconstituer des formes convexes, que pour ce qui concerne les puzzles à 5 pièces. Pour les puzzles à 7 pièces, comme le Tangram et la plupart des puzzles historiques, les puzzles qui reconstituent le maximum de formes convexes sont des dissections du carré d'aire 32 ou 36 vraisemblablement. Les formes convexes obtenues avec ces puzzles de grande aire sont de moins en moins faciles à distinguer. Voyez ci-dessous les 60 formes convexes obtenues avec une dissection à 10 pièces d'aire 64.



