Dans cette section, nous traiterons d'un jeu très peu complexe : le jeu des allumettes et de la stratégie pour gagner à tout les coups puis nous triterons d'une variation un peu plus complexe à ce jeu
Tout d’abord, le jeu des allumettes est un jeu dans lequel on dispose de n allumettes alignés, avec un n entier naturel, et où les 2 joueurs qui s’affrontent doivent chacun leur tour décider de retirer 1,2 ou 3 allumettes. Celui qui retire la dernière allumettes perd la partie.
Tentez d'affronter l'ordinateur dans une partie avec 13 allumettes en cliquant sur les allumettes pour les enlever.
Comme vous pouvez le voir, il est impossible de gagner contre l'ordinateur dans cette situation. Sa stratégie est "parfaite". En effet, le nombre d'allumettes qu'il enlève n'est pas aléatoire mais il a une explication mathématique
Résumons d’abord dans un tableau le nombre d’allumettes que nous devons retirer pour gagner:
Allumettes: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 ...
J’en prends:P 1 2 3 P 1 2 3 P 1 2 3 P 1 …
Nous observons en faisant la division euclidienne d’un nombre d’allumettes pour lesquelles je perd forcément 4, le reste est de 1. On est alors ramené au cas dans lequel on dispose d’une allumette en face de nous. Ensuite, en faisant la division euclidienne d’un nombre d’allumettes pour lesquelles j’en prend 1 par 4, le reste est de 2. On est alors ramené au cas dans lequel on dispose de 2 allumettes en face nous. Puis, en faisant la division euclidienne d’un nombre d’allumettes pour lesquelles j’en prend 2 par 4 le reste est de 3. On est alors ramené dans le cas de figure où nous disposons de 3 allumettes en face nous. Enfin, en faisant la division euclidienne d’un nombre d’allumettes pour lesquelles j’en prend 3 par 4, le reste est nul. On est alors ramené au cas où on dispose de 4 allumettes en face de nous.
Nous en concluons donc que si le reste de la division du nombre d’allumettes restant par 4 est nul, alors il faut prendre 3 allumettes. S’il est de 1, alors on a perdu si on considère que le joueur adverse joue parfaitement. S’il est de 2, alors il faut prendre 1 allumettes. S’il est de 3, alors il faut en prendre 2.
Dans une situation à 4n+1 allumettes si vous jouez en deuxième, il faut donc jouer en complément à 4 par rapport au coup précédent de l'adversaire. S'il prend 1 allumettes : vous en prenez 4-1=3 ; s'il en prend 2, vous en prenez 4-2=2... C'est ici la simple stratégie qu'utilise l'ordinateur pour gagner à tous les coups.
On peut complexifier le jeu des allumettes en y ajoutant une deuxième dimension, créant ainsi plusieurs rangées d’allumettes de cette manière:
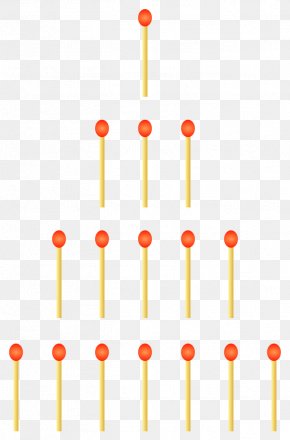
Ce jeu est appelé jeu de Marienbad popularisé par le film L'Année dernière à Marienbad, en 1961. Ses règles sont les mêmes que le jeu des allumettes en 1 dimensions à l'exception d’une règle: on peut prendre un nombre quelconque d'allumettes mais dans une seule rangée. Le nombre de rangées et le nombre d’allumettes par rangée peut être réglable et il existera toujours une stratégie gagnante.
Pour commencer, il faut representer en binaire le nombre d'allumettes à chaque rangée.
Dans notre exemple, on peut écrire:
1
11
101
111
On additionne ensuite chaque ligne.
Dans notre cas, on a 1+11+101+111=224
Penons queslques exemple:
Si le premier joueur prend l'allumettes de la première rangée, on a: 11+101+111=223
On peut prendre une allumette de la 2e ou 3e rangée pour avoir 222 et garder une position gagnante
Si le premier joueur prend toute la dernière première rangée, on a: 1+11+101=113
Il faut alors enlever 101 et ajouter 10. On enlève donc 3 allumettes de la dernière rangée pour obtenir 1+11+10=22 qui est une position gagnante.